Indoor positioning is a very popular topic recently, mostly due to the iBeacon technology promoted by Apple, and adopted by other vendors. Most of the research on indoor location involves a set of fixed beacons on well-known positions, and a moving beacon signal receiver. What if the beacon was moving, and the receivers were fixed?

Such a scenario can have many uses, where it is beneficial that the positioned object is as simple as possible, e.g. tracking shopping cart movement in a mall. It is much easier to equip each cart with a beacon, than with a device capable of calculating the distance.

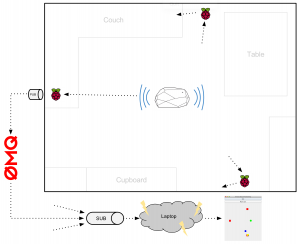
In my setup, I was tracking movement of an Estimote beacon with the help of three Raspberry Pi agents placed in my living room (which is about 4m x 5m wide). Each Raspberry Pi is equipped with:

• an IO-Gear GBU521 Bluetooth 4.0 Micro Adapter
• a TP-LINK WN725N WiFi dongle

The RPis listen to all Bluetooth Low-energy advertisement packets, and send them to a ZeroMQ pub socket. That part of the code is in C, and partly follows hcitool from bluez. ZeroMQ was a good fit here because of its ease of use and many language bindings (including C and Java). You also don’t have to worry about connecting or reconnecting, the publishers and subscribers can be started and stopped at any time, and things work as expected.

On the other end, a Scala-based GUI subscribes to the three RPi publishers (ZeroMQ sub socket), parses and filters the packets (not all advertisements are in the iBeacon format) and feeds them to the positioning algorithms. The results are then displayed on the screen.

Each agent receives about 7-10 advertisement packets (and RSSI measurements) per second from each beacon.

I implemented two approaches to positioning. The first is based on trilateration. Basing on the measured RSSI, it is possible to approximate the distance to the beacon, and hence determine a circle, on which the beacon must be. Having three such measurements, it is possible to estimate the position in a 2D plane. As the readings aren’t exact, and there’s most probably no unique intersection point, I used the SimplexOptimizer from commons-math, to determine a point from which distance to the three circles is minimal.

To accomodate for temporary signal strength variations, I used an average of the 10 last readings of the RSSI per agent.

The second approach uses a neural network. First, I placed the beacon at a couple of well-known locations (storing the coordinates of that location), and stored the stream of measurements for a minute. Repeating the process several times, I got about 7 thousand training examples (tuples of three measurments from three different agents and the real location). Then I trained a neural network, implemented using Encog; I got the smallest error when the input contained 4 most recent readings per agent (so 12 inputs), and the single hidden layer had 80 neurons. The output was a pair of coordinates.

You can see the results on the video below:

• the red squares are the fixed agents, receiving the beacon signals
• the green circle is the position of the beacon as estimated by trilateration
• the blue circle is the position as estimated by the neural network approach
• the yellow square is the target location to which I am currently moving the beacon

Initially the beacon is in the center. Then I’m marking the position where the beacon is going to be moved, and move the beacon.

As you can see, the results are not very accurate. The neural network learned very well when the beacons are very close to an agent, but gives erroneous results when it is further away. On the other hand, trilateration works much better when the beacon is at some distance from the agents (you can see the movement when it happens), but fails to capture the fact the a beacon is very close to a given agent.

To sum up, while this approach cannot be used to precisely determine the location of a beacon, it can be used to get a rough estimation on where the beacon is. Also certainly both the neural network, and the trilateration algorithm can be improved for better accuracy, and the results combined to get a better approximation. Other approaches, like particle filtering, could be implemented as well.

Update: raw data containing RSSI measurements and approximate beacon positions is available here.